In the last post, I presented a COVID-19 model in which a curve-fitting model was used to fit the number of COVID-19 cases in North Carolina. One of the problems with modeling the number of COVID-19 cases at this early stage is that it is nearly impossible to know with any degree of certainty how many individuals were exposed but had minimal to no symptoms, and have not been tested. A recent Stanford University study suggests that the current count of cases may only represent 20-50% of the total number of individuals that have been exposed. For this reason, models of the number of deaths may be more useful in guiding reopening decisions.
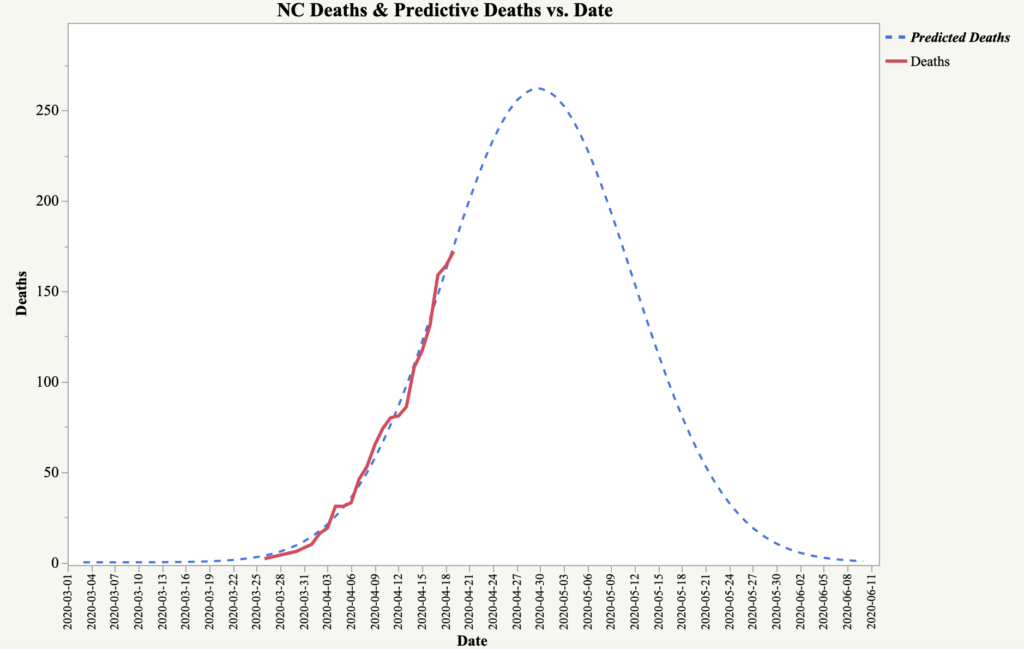
The following is a Gaussian Peak model of the number of reported COVID-19 deaths for the state of North Carolina as of April 18, 2020. Based on this model, it appears that the state of North Carolina will not reach a peak in the number of deaths due to COVID-19 until around May 1st. What is interesting is that based on this model, deaths will peak at the same time as the expected cases derived in the previous model. Based on the Stanford study referenced above, this would suggest the fatality to cases rate is much lower than projected. This does not negate the fact that there has been a significant number of deaths, instead, it simply suggests that more individuals than originally thought have been exposed to the virus.
Unfortunately, there are limitations to the models presented up to this point. One important limitation is that they do not allow for ‘what-if” scenarios. In the current COVID-19 environment, policymakers at all levels continue to struggle with “stay-at-home” orders, social distancing, and reopening decisions. What would help would be a model which allows policymakers to test different actions to see how they may influence the spread of COVID-19. Luckily, epidemiological models exist for this very purpose. The simplest of these is the SIR model.
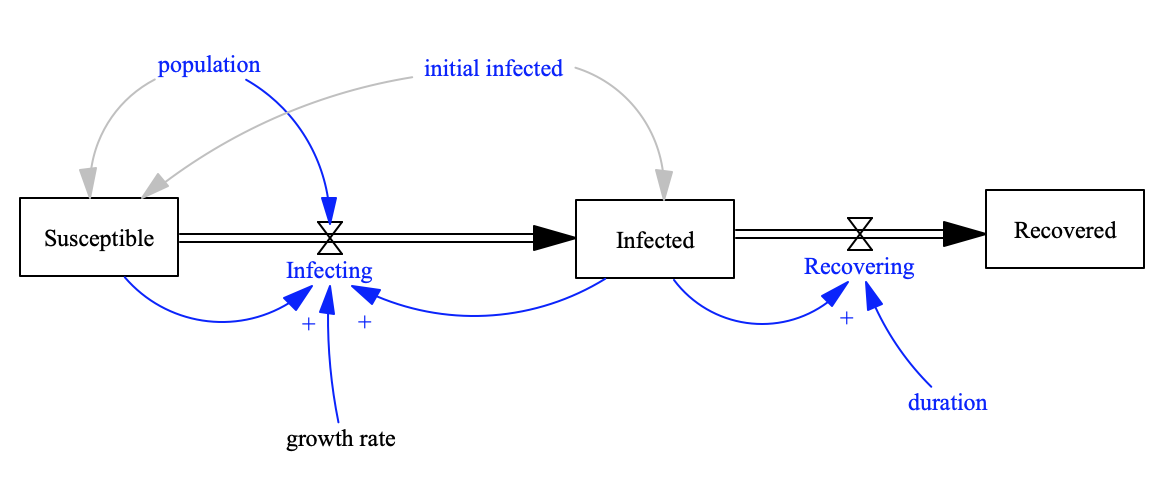
In the next post, I will elaborate on the SIR model and the slightly more complex SEIR model which is designed to taking into consideration the interaction between factors such as the number susceptible, the number inflected, and the number of people recovering.